【人教版·初中·图形与几何模块】

　　相交线

　　课型：新授课

　　课时：1课时

　　教学目标：

　　1.知识与技能目标

　　知道对顶角和邻补角的概念;掌握对顶角的性质及其推导过程。

　　2.过程与方法目标

　　通过动手操作、自主探究的过程，学生的动手能力和探究能力得到提高。

　　3.情感、态度与价值观目标

　　激发学习兴趣。

　　教学重点：

　　对顶角和邻补角的概念;掌握对顶角的性质。

　　教学难点：

　　对顶角的性质的推导过程。

　　教学工具：多媒体课件、剪刀、白纸

　　教学过程：

　　一、情境引入

　　展示剪刀剪纸的过程，并请学生注意观察剪刀在剪纸的过程中有关角的变化，提问：你能发现什么?如果将剪刀的构造看作两条相交的直线，这是关系到什么问题?引出相交直线所成角的问题。

　　二、探究新知

　　1.请学生在纸上任意画两条相交直线，形成四个角，将四个角依次标上1，2，3，4，则∠1和∠2有怎样的位置关系?∠1和∠3呢?

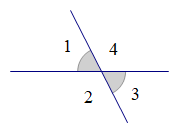
　　2.分别量一下各个角的度数，∠1和∠2的度数有什么关系?∠1和∠3呢?在刚刚老师演示的剪刀把手之间的角变化的过程中，这个关系还存在吗?

　　学生动手操作，小组讨论交流，教师巡视。

　　3.学生回答：∠1和∠2有一条公共边，它们的另一边互为反向延长线，即∠1和∠2互补;∠1和∠3有一个公共顶点，并且∠1的两边分别是∠3的两边的延长线。教师评价，并给出邻补角和对顶角的概念。

　　4.根据刚才量得的角的度数，你能发现什么?可以证明你的结论吗?小组讨论，全班交流。

　　5.学生回答，教师总结对顶角的性质：对顶角相等。给出推导过程：因为∠1与∠2互补，∠3与∠2互补(邻补角的定义)，所以∠1=∠3(同角的补交相等)。

　　三、巩固练习

　　如下图，直线a、b相交，∠1=40度，求∠2，∠3，∠4的度数。

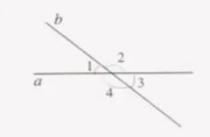
　　四、课堂小结

　　这节课大家有什么收获和体会?

　　五、课后作业

　　课后练习第1题、第2题。

　　板书设计：

　　相交线

　　1.互补角

　　2.对顶角

　　3.对顶角的性质：对顶角相等