【人教版·初中·数与代数模块】

　　二元一次方程组

　　课型：新授课

　　课时：1课时

　　教学目标：

　　1.知识与技能目标

　　理解二元一次方程、二元一次方程组以及它们的解的概念。

　　2.过程与方法目标

　　结合实例，通过自主探究，学生能提高分析问题和解决问题的能力。

　　3.情感、态度与价值观目标

　　感受数学来源于生活又服务于生活，体会数学建模思想。

　　教学重点：

　　二元一次方程、二元一次方程组以及它们的解的含义，能够检验一组数是否是二元一次方程(组)的解。

　　教学难点：

　　理解二元一次方程组的解的含义。

　　教学工具：多媒体课件

　　教学过程：

　　一、创设情境，引入新课

　　1.结合生活实例，提问：同学们喜欢看篮球比赛吗?在一场篮球联赛中，每场比赛都要分出胜负，每队胜1场得2分，负1场得1分。某队在10场比赛中得到16分，那么这个队胜负场数分别是多少?你能列出方程吗?

　　学生可根据题意列出一元一次方程。

　　2.在列一元一次方程时需要用一个未知数表示另一个未知数，能不能根据题意直接设两个未知数，使列方程变得容易呢?

　　二、探究新知

　　(一)二元一次方程(组)的概念

　　1.教师继续提问：刚刚的问题包含了哪些必须同时满足的条件?设胜的场数是

　　，负的场数是y，你能用方程把这些条件表示出来吗?

　　学生独立思考，尝试列出方程。指名学生回答问题，题中包含两个必须同时满足的条件：胜的场数+负的场数=总场数，胜场积分+负场积分=总积分。由以上条件可列方程：x+y=10，2x+y=16。

　　2.教师提问：这两个方程有什么特点?与一元一次方程有什么不同?

　　学生观察两个方程，并与一元一次方程相比较。发现：上面两个方程，每个方程中都含有两个未知数，并且含有未知数的项的次数都是1。

　　教师总结：像这样的方程叫做二元一次方程。

　　3.教师讲解：上述问题中包含两个必须同时满足的条件，即两个未知数必须同时满足方程x+y=10和2x+y=16，将这两个方程合在一起，写成

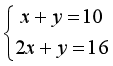
　　，就组成一个方程组。

　　4.根据刚刚列出的方程组，大家发现它有什么特点吗?

　　学生观察发现：①方程组中有两个未知数;②每个未知数的项的次数都是1;③一共有两个方程。

　　教师总结：有以上特点的方程组，叫做二元一次方程组。

　　(二)二元一次方程(组)的解

　　1.满足方程x+y=10，且符合问题实际意义的x，y有哪些?请将它们填写在教材P89的表格中。

　　2.表格中哪对x，y的值还满足方程2x+y=16?

　　学生填写表格，独立思考。同桌之间相互交流，回答问题。

　　教师归纳：一般地，使二元一次方程两边的值都相等的两个未知数的值，叫做二元一次方程的解。二元一次方程组的两个方程的公共解，叫做二元一次方程组的解。

　　三、巩固练习

　　加工某种产品需经两道工序，第一道工序每人每天可完成900件，第二道工序每人每天可完成1200件。现有7位工人参加这两道工序，应怎样安排人力，才能使每天第一、第二道工序所完成的件数相等?

　　四、课堂小结

　　这节课大家有什么收获和体会?

　　五、课后作业

　　课后练习第1、2两题。

　　板书设计：

　　二元一次方程组

　　1.二元一次方程(组)的概念

　　①二元一次方程：每个方程中都含有两个未知数，并且含有未知数的项的次数都是1。

　　②二元一次方程组：方程组中有两个未知数，每个未知数的项的次数都是1，并且一共有两个方程。

　　2.二元一次方程(组)的解

　　①二元一次方程的解：使二元一次方程两边的值都相等的两个未知数的值。

　　②二元一次方程组的解：二元一次方程组的两个方程的公共解。