2024年重庆公务员考试2024年3月11日-3月16日打印准考证。华图教育同步重庆公务员考试论坛更新2024年重庆公务员考试准考证打印入口,考生可从下方进入打印准考证。友情提醒,记得多打印几张准考证,以备不时之需。
>>>点击2024重庆公务员考试准考证打印入口<<<
【 2024重庆公务员考试历年分数线-试题-资料】
【↓↓扫码领取 ↓↓】

2024重庆公务员考试打印准考证必读
1.在规定的时间内登录重庆市人力资源和社会保障局首页,点击左方“人事考试网上报名”进入。点击相应考试名称进入该考试专题,点击打印准考证。
2.点击‘打印预览’可预览准考证样式。
3.打印机无所谓黑白或彩色,只要字迹清晰,照片能辨认即可。
4.如遇到网络繁忙,或考生电脑网速太慢而导致准考证上相片无法正常显示,请对网页进行刷新,直到能正常显示相片方可打印。或者避开网络高峰期,选择凌晨时段进行打印。
5.打印不分正反两面,直接打印成一张A4纸即可。
6.如考生无网上打印条件,可于打印准考证时间段内,打电话咨询或者当地人事考试机构进行打印。
7.准考证打印时间:2024年3月11日上午9:00至3月16日上午9:30
在规定的时间打印准考证,否则过了时间没有办法打印。
8.准考证上的信息与我报考填写的信息不一样?
考生在打印前,应该认真核对准考证上身份证号码、报考部门名称及代码、职位名称及代码等与所报考的信息是否一致。如有错误的考生本人应及时跟所在考区的公务员考试机构联系解决。
9.打印格式不对信息有错怎么办?
建议适用IE浏览器下载准考证
2024重庆公务员考试笔试科目、时间和地点
1. 内容。笔试包括公共科目和专业科目。公共科目包括行政职业能力测验和申论两科。其中,行政职业能力测验为客观性试题,申论为主观性试题,满分均为100分,详见《重庆市2024年度公开考试录用公务员公共科目考试大纲》。申论试卷分为“申论1”、“申论2”和“申论3”,行政执法类职位申论考试类型为“申论3”,乡镇机关职位申论考试类型为“申论2”,其他职位申论考试类型为“申论1”。
>>>免费领取2024重庆市考考前30分资料<<<
报考公安人民警察执法勤务职位的,还须参加公安类专业科目考试,分值100分,考试大纲可在报名网站查询。笔试成绩按照行政职业能力测验、申论、专业科目考试成绩分别占40%、30%、30%的比例合成。
报考法院系统、检察机关职位的,还须参加法律基础知识考试,分值100分,考试大纲可在报名网站查询。笔试成绩按照行政职业能力测验、申论、专业科目考试成绩分别占40%、30%、30%的比例合成。
报考其他职位的,笔试成绩按照行政职业能力测验、申论各占50%的比例合成。
2. 时间。公共科目笔试时间为2024年3月16日,专业科目笔试时间为2024年3月17日。具体安排为:
3月16日上午 9:00—11:00 行政职业能力测验
下午 14:00—16:30 申论
3月17日上午 9:00—11:00 公安类专业科目
上午 9:00—10:00 法律基础知识
报考者应当按照准考证上确定的时间和地点,同时携带准考证和本人有效居民身份证(与报名时一致)参加考试。
>>>扫码查看考点分布图<<<

——重庆公务员考试备考——
重庆市考数量关系备考技巧:赋值法和方程法在工程问题中的应用
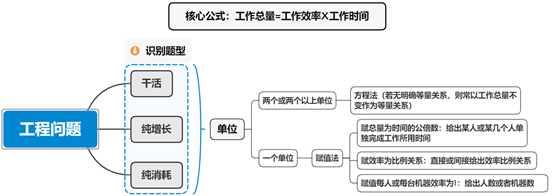
众所周知,在工程问题解题中常用的方法有赋值法和方程法,一般来说方程法和赋值法都是分别应用,我们对于方程法和赋值法的区分如下:当题中给出工作总量、工作时间、工作效率三类量中的两类或三类具体值,使用方程法;反之,一般只给出工作时间这一类具体值,则使用赋值法。
但是,结合近几年公务员考试的真题来看,单纯使用赋值法或方程法,不能帮助我们解决所有的工程问题,很多时候需要将赋值法和方程法结合起来。那么接下来我们通过一些例题,来探究如何将两种方法结合在一起解决工程问题。
【例1】现有一批零件,甲师傅单独加工需要4小时,乙师傅单独加工需要6小时。两人一起加工这批零件的50%需要( )小时。
A.0.6
B.1
C.1.2
D.1.5
【答案】C
【解析】赋值工作总量题干中只有工作时间这一类具体值,故使用赋值法。赋值工作总量为时间的公倍数24(4和6的公倍数),则甲、乙两人的工作效率分别为6与4。题中问加工这批零件的50%需要多少小时?即加工零件24×50%=12。两人合作时,效率为6+4=10,根据工作总量=工作效率×工作时间,设需要时间为t,则12=10×t,解得t=1.2小时。
【总结】在解决本题时,最后一步很多考生在计算时通过工作总量=工作效率×工作时间,则工作时间=工作总量/工作效率,直接代入数据可得工作时间为小时。然则通过我们刚才解析所列,最后一步其实用到了方程的一个思想,故而我们在解决工程问题时,已经是将方程法和赋值法同时应用。
【例2】某商铺甲乙两组员工利用包装礼品的边角料制作一批花朵装饰门店。甲组单独制作需要10小时,乙组单独制作需要15小时,现两组一起做,期间乙组休息了1小时40分,完成时甲组比乙组多做300朵。问这批花有多少朵?
A.600
B.900
C.1350
D.1500
【答案】B
【解析】题干中给出甲乙分别单独制作完成所需时间,我们可以赋值工作总量为10和15的公倍数30,此时甲组与乙组的效率分别为3和2。由于题干最终的要求需要我们求出具体这批花朵的数量,故我们赋值的工作总量30仅为30份,需要求解一份具体为多少朵花,我们可以设每份花朵为x,即工作总量为30x,甲组与乙组的效率分别为3x和2x。
实际工作时,乙组休息了1小时40分钟即53小时,这53小时只有甲组在工作,其余时间为两组合作。甲组工作5/3小时,工作量为3x×5/3=5x,剩余30x-5x=25x的工作量为甲乙两组合作,所需时间为25x÷(2x+3x)=5小时,即乙组工作时间为5小时,甲组工作时间为5+53=203小时,根据“完成时甲组比乙组多做 300 朵”,可得甲组工作量-乙组工作量=300朵,即3x×203-2x×5=300,解得x=30(朵),这批花一共有30x=30×30=900朵。因此,选择B选项。
【总结】在本题中,出现工作时间和工作总量这两类具体值,很多考生的第一反应应该用方程法解题,但是实际我们实际赋值了工作总量为30份,设每一份为x,最终令工作总量为30x,也将方程法和赋值法结合了起来。
综上所述,原先方程法和赋值法在工程问题中应用的区别主要看单位的个数,工程问题中共有3类量,如果有两类及以上的量带有具体单位,那么我们用方程法,反之则应用赋值法。通过上述两道题目的解析,我们可以看出,在解决工程问题时,只要题目满足可应用赋值法的某些条件(比如说,题干中给出某些主体单独完成工作所用时间;给出各个主体的效率比例关系),我们便可以赋值总量或者效率,此时所赋值的总量或者效率单位即为份数,如果题干中给出的总量或者效率带有具体单位,则此时应将每份设为x,这就是将赋值和方程结合在一起的应用,各位备考考生可以自行去寻找相关的题目进行练习。
在了解相关国考信息后,考生可积极备考24年国家公务员考试,成功的关键是有效的备考!












