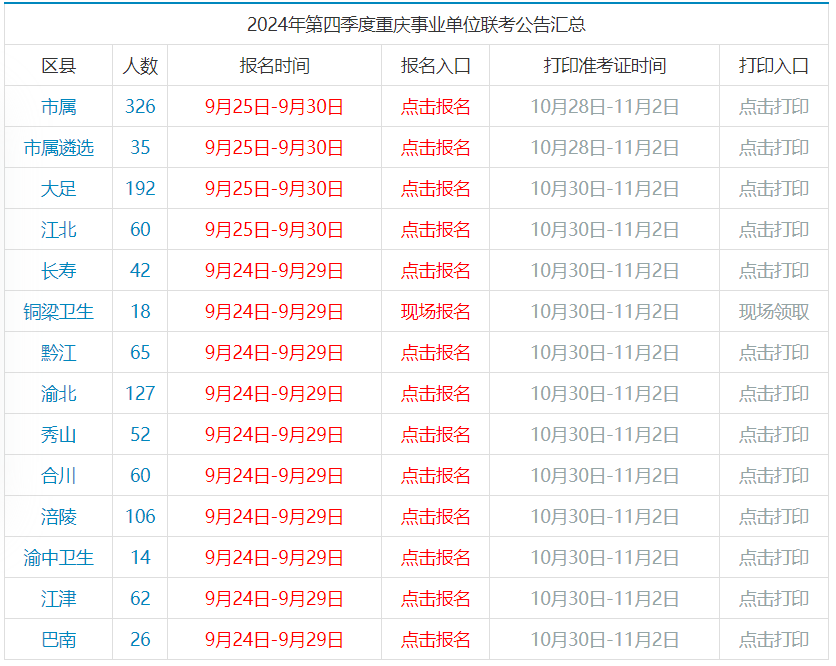
点击打印:2024年重庆事业单位11月2日准考证打印入口汇总
扫一扫,咨询重庆事业单位考试备考资料,附件下载 疑问解答

免费领取,重庆事业单位ABCE类笔试备考资料

重庆1102事业单位联考公告!你是不是还不清楚自己该备考哪一类?图图就来给大家详细讲讲各类的区别。注意,以下内容仅供参考,最终备考内容以实际岗位表上面的类别为主!
01、综合管理类(A类)
适用于
事业单位中以行政性、事务性和业务管理为主的岗位。
招聘专业主要有
工商管理类、法律类、中国语言文学类、经济学类、汉语言文学类、会计与审计类、新闻传播学类、财务管理类、计算机科学与技术、电子商务、工商管理及市场营销、工业工程、公共管理、管理科学与工程、旅游管理、农林管理、物流管理与工程、财政税务、金融、经济贸易与管理、人力资源管理、安全生产、材料学、计算机、统计学、专业不限等。
笔试内容
《职业能力倾向测验(A类)》分为:常识判断+言语理解与表达+数量关系+判断推理+资料分析,各科目分值共150分。
《综合应用能力(A类)》试卷由注意事项、背景材料和试题三部分组成,全部是主观性试题。试题内容主要涉及事业单位管理岗位典型的工作任务,如观点归纳、资料分类、草拟信函、会务安排、应急处理、联络通知等。主要为案例分析题和应用文写作题两大类型。
02、社会科学专技类(B类)
适用于
事业单位人文社科类专业技术岗位。比如经济、新闻、出版编辑、公证员、馆员、会计、广电播音、工艺美术等岗位。
招聘专业主要有
会计学、体育学、教育学、历史学、外国语言文学、新闻出版、数字媒体艺术等相关专业、哲学、中国语言文学、美术及摄影、设计学、舞蹈学、戏剧与影视、艺术理论、音乐学、法学、民族学、社会学、政治学类、马克思主义理论类等。
笔试内容
《职业能力倾向测验(B类)》分为:常识判断+言语运用+数量分析+判断推理+综合分析,各科目分值共150分。
《综合应用能力(B类)》试卷由主观性试题组成,主要题型包括概念分析题、校阅改错题、论证评价题、材料分析题和写作题等。每次考试从上述题型中组合选用。
03、自然科学专技类(C类)
适用于
事业单位自然科学类专业技术岗位。比如工程、农技、统计、民航飞行、关务员、实验员、技工学校教师等岗位。
招聘专业主要有
计算机科学与技术、水利水电工程、植物生产类、土木工程、土木类、农业工程类、化学类、机械设计制造及其自动化、建筑学、农学、农业技术类、大气科学类、机械类、水利类、生物学、食品科学及工程、数学、水利水电水工、天文及大气科学、统计学、物理学、公安技术等。
笔试内容
《职业能力倾向测验(C类)》分为:常识判断+言语运用+数量分析+判断推理+综合分析,各科目分值共150分。
《综合应用能力(C类)》试卷以主观性试题为主,主要题型包括科技文献阅读题、论证评价题、科技实务题、材料作文题等。每次考试从上述题型中组合选用。
04、中小学教师类(D类)
适用于
中小学(含幼儿园)和中专等教育机构的教师岗位。
笔试内容
《职业能力倾向测验(D类)》分为:言语理解与表达+数量分析+判断推理类比推理+策略选择,各科目分值共150分。
《综合应用能力(D类)》试卷主要题型包括辨析题、案例分析题、教育方案设计题等,旨在测查应试人员综合运用教育学、心理学等相关知识和技能,分析、解决中小学教育教学问题的能力。
05、医疗卫生类(E类)
适用于
医疗卫生机构专业技术岗位。比如临床、护理、放射师等岗位。
招聘专业主要有
基础医学类、预防医学类、卫生管理类、临床医学类、医学技术类、口腔医学类、中医学类、护理学类、药学类等。
笔试内容
《职业能力倾向测验(E类)》包括常识判断、言语理解与表达、数量分析、判断推理、策略选择等部分。
《综合应用能力(E类)》试卷主要由医学基础知识和招聘岗位专业知识应用能力两个部分组成。其中,医学基础知识部分占比60%,所有应试人员必答;招聘岗位专业知识应用能力部分占比40%,具体分为中医临床、西医临床、药剂、护理、医学技术、公共卫生管理六个类别,应试人员应根据报考岗位选做相应类别的试题。
目前,重庆1102事业单位联考公告陆续发布中,明日将开启报名入口,大家可以具体查看职位表里面的类别,还没有心仪岗位,仍在等公告的同学可以先参考上文内容选择对应的类别来备考。
重庆事业单位职业能力倾向测验:数量关系之余数问题
在整数的除法中,有能整除与不能整除两种情况。当不能整除时,就产生余数。余数问题一直是数量关系考试学习中的难点,尤其是余数问题涉及到除法运算。除法运算在很多学习者眼中是比较麻烦而且容易出错的,但其实在真正考试中遇见余数问题一般用代入排除法。
代入排除法是如何运用在余数问题中的,通过下面的例子来说明:
【例1】疫情期间,爱心人士向某街道捐赠了两箱防疫物资,内装物资件数相同。街道将两箱物资分别给了甲、乙两个工作组,其中甲工作组除1人拿到4件物资外,其余每人各分得5件;乙工作组除1人拿到6件物资外,其余每人各分得7件。已知每箱物资数量在50到100件之间,则每箱装有防疫物资( )件。
A.58 B.62
C.69 D.74
【答案】C
【解析】第一步,本题考查余数问题。
第二步,甲组除1人拿到4件物资外,其余人都拿5件,说明物资总数除以5应余4,代入选项验证,排除A和B选项;乙组除1人拿到6件物资外,其余人都拿7件,说明物资总数除以7应该余6,代入C和D选项验证,只有C选项满足。
因此,选择C选项
【例2】某镇政府办公室集中采购一批打印纸,分发给各个职能部门。如果按每个部门4包分发,则多6包;如果按每个部门5包分发,则有1个部门只能分到3包。这批打印纸的数量是:
A.38包 B.36包
C.40包 D.42包
【答案】A
【解析】第一步,本题考查余数问题,用代入排除法解题。
第二步,代入A选项,38÷4=8……6,即8个职能部门,每个部门得到4包还剩6包;38÷5=7……3,即8个职能部门,其中7个部门每个部门得到5包,还剩一个部门分到3包;两个条件均满足,满足题意;代入B选项,36÷4=9,不满足题意,排除;代入C选项,40÷4=10,不满足题意,排除;代入D选项,42÷4=9……6,42÷5=8……2,不满足题意,排除。
因此,选择A选项。
可见,代入排除法可以解决绝大多数余数问题。但余数问题其实还常用同余口诀来解题。
“余同取余,和同加和,差同减差,公倍数作周期。”
举例来说:
(1)余同:“一个数除以4余1,除以5余1,除以6余1”,则取1,表示为60n+1;
(2)和同:“一个数除以4余3,除以5余2,除以6余1”,则取7,表示为60n+7;
(3)差同:“一个数除以4余1,除以5余2,除以6余3”,则取-3,表示为60n-3。
选取的这个数加上除数的最小公倍数的任意整数倍(即例中的60n)都满足条件。
前面例题1和例题2均可以利用同余口诀来解决。
以例题1说明:“甲工作组除1人拿到4件物资外,其余每人各分得5件;乙工作组除1人拿到6件物资外,其余每人各分得7件”,转化一下信息即:一个数除以5余4,除以7余6,差同取-1,除数的最小公倍数是35,总体表示为35n-1,当n=2时,即为正确选项C。
以例题2说明:“如果按每个部门4包分发,则多6包;如果按每个部门5包分发,则有1个部门只能分到3包”,转化一下信息即:一个数除以4余2(题目中多6包,还能除以一次4),除以5余3,差同取-2,除数的最小公倍数为20,总体表示为20n-2,当n=2时,即为正确选项A。
无论是代入排除法还是同余口诀,运用熟练余数问题就不是难题。在考试中,考生可以因题制宜,优先选择代入排除法,但是同余口诀的原理也应当有所了解。











