2024重庆公务员考试公告已出!速查!此次2024重庆公务员考试招录4530人,报名时间为2024年2月1日上午9:00至2月6日上午9:00,考试时间定在3月16日。考生可从下方链接进入直接查询2024重庆公务员考试公告!重庆市考职位表信息也可从下方进入查询!小编在此祝各位考生顺利上岸重庆市考!
>>>点击报名入口<<<

报考者可在2024年2月1日上午9:00至2月6日上午9:00期间登录报名网站提交报考申请,报考者只能选择一个部门(单位)中的一个职位进行报名,报名与考试时使用的本人有效居民身份证必须一致。
报名时,报考者须承诺诚信报考,提交的报名信息和材料必须真实、准确、完整,报考者在提交报名信息前,请再次认真核对本人所填信息是否准确,是否符合招考公告及招考职位资格条件,避免误报。
附件点击查看
>>>点击查看2024年重庆省公务员考试公告<<<
扫码职位表下载

2024年重庆考历年进面分数线、历年试题及解析、备考资料包

一、2024重庆公务员考试报考职位查询
各招录机关的具体职位、资格条件等信息详见《重庆市2024年度考试录用公务员职位表》,报考者可通过相关网站查询招考职位信息。招考职位的专业、学历、学位等有关资格条件问题,由各市、省直管县和省直各招录机关负责解释(咨询电话见职位表)。有关报考政策、报名网络技术和考务安排等事宜,请参阅《重庆市2024年度考试录用公务员报考指南》(以下简称《报考指南》)。
二、2024重庆公务员考试报考条件
(一)基本要求
1. 具有中华人民共和国国籍;
2. 年龄为18周岁以上、35周岁以下(1988年2月至2006年2月期间出生),2024年应届硕士、博士研究生年龄可放宽到40周岁以下(1983年2月以后出生);
报考人民警察(含公安人民警察、监狱戒毒人民警察、司法警察)职位的,年龄为18周岁以上、30周岁以下(1993年2月至2006年2月期间出生);2024年应届硕士、博士研究生和报考法医、狱医、所医职位的,年龄放宽到35周岁以下(1988年2月以后出生);
3. 拥护中华人民共和国宪法,拥护中国共产党领导和社会主义制度;
4. 具有良好的政治素质和道德品行;
5. 具有正常履行职责的身体条件和心理素质;
6. 具有符合职位要求的工作能力;
7. 具有大学专科及以上文化程度;
8. 具备重庆市公务员主管部门规定的拟任职位所要求的其他资格条件。
(二)其他要求
1. 国内普通高等院校应届毕业生须于2024年7月31日前取得相应毕业证书和学位证书;其他报考者须于2024年2月29日前取得相应毕业证书和学位证书,留学回国人员还须在2024年2月29日前通过教育部留学服务中心学历学位认证。招考职位所要求的其他资格条件均应在2024年2月29日前取得。
2. 市级机关除部分特殊职位和专业性较强的职位外,主要招录具有2年以上基层工作经历的人员,区县级及以下机关主要招录应届高校毕业生。基层工作经历计算时间截止2024年2月。
3. 对艰苦边远地区的乡镇机关职位,可以采取降低学历要求、放宽专业条件、不限制工作年限和经历、降低笔试开考比例、单独划定笔试合格分数线等措施,适当降低进入门槛。对于通过降低进入门槛等倾斜政策录用的人员,应当在所报考区县辖区范围内的艰苦边远地区乡镇机关最低服务5年(含试用期);未满5年的,不得交流(含公开遴选)到除本区县艰苦边远地区乡镇机关以外的其他机关。对非艰苦边远地区的乡镇机关职位,新录用人员应当在乡镇机关最低服务5年(含试用期)。
4. 面向服务基层项目人员招考的,其对象是指我市服务期满并经考核合格的“三支一扶”计划(本科生服务期满2年及以上,研究生服务期满1年及以上)、“农村义务教育阶段学校教师特设岗位计划”(服务期满3年及以上)、“大学生志愿服务西部计划”(服务期满2年及以上)服务基层项目人员和入伍地、退伍地或户籍地为重庆市辖区的服现役满5年的高校毕业生退役军人。另外,在艰苦边远地区工作满3年且历年考核为合格以上等次的在编在岗事业编制人员,可以报考本区县面向服务基层项目人员定向招考的职位。
5. 现役军人、在读的非应届毕业生、在职公务员和参照公务员法管理的机关(单位)工作人员,不能报考。
因犯罪受过刑事处罚的人员、被开除中国共产党党籍的人员、被开除公职的人员、被依法列为失信联合惩戒对象的人员,在各级公务员招考中被认定有舞弊等严重违反录用纪律行为的人员,公务员和参照公务员法管理的机关(单位)工作人员被辞退未满5年的,以及法律规定不得录用为公务员的其他情形的人员,不得报考。
报考者不得报考录用后即构成公务员法第七十四条第一款所列情形的职位,也不得报考与本人有夫妻关系、直系血亲关系、三代以内旁系血亲关系以及近姻亲关系的人员担任领导成员的用人单位的职位。
三、2024重庆公务员考试报名
本次招考采取网上报名方式,报考者登录重庆市人力资源和社会保障局网站(https://rlsbj.cq.gov.cn)首页“我要办”中的“人事考试网上报名”栏目,点击“2024年重庆市公务员招录考试网上报名入口”进入报名系统,具体按照以下程序进行:
1. 提交报考申请。报考者可在2024年2月1日上午9:00至2月6日上午9:00期间登录报名网站提交报考申请,报考者只能选择一个部门(单位)中的一个职位进行报名,报名与考试时使用的本人有效居民身份证必须一致。
报名时,报考者须承诺诚信报考,提交的报名信息和材料必须真实、准确、完整,报考者在提交报名信息前,请再次认真核对本人所填信息是否准确,是否符合招考公告及招考职位资格条件,避免误报。
为方便广大报考者了解各个职位的报名情况,重庆市人事考试中心将从报名开始日的第2天(2月2日)起至2月4日止,每天上午11:00左右,在重庆市人力资源和社会保障局网站首页“重庆市2024年度考试录用公务员专栏”,公布各职位报名相关数据。此后,不再公布每日报名数据,待缴费结束后再公布最终报名数据。
为防止大量报考者集中在临近报名结束时报名,造成网络拥堵,请报考者审慎把握报名时间。
四、2024重庆公务员考试报名笔试
(一)笔试
1. 内容。笔试包括公共科目和专业科目。公共科目包括行政职业能力测验和申论两科。其中,行政职业能力测验为客观性试题,申论为主观性试题,满分均为100分,详见《重庆市2024年度公开考试录用公务员公共科目考试大纲》。申论试卷分为“申论1”、“申论2”和“申论3”,行政执法类职位申论考试类型为“申论3”,乡镇机关职位申论考试类型为“申论2”,其他职位申论考试类型为“申论1”。
报考公安人民警察执法勤务职位的,还须参加公安类专业科目考试,分值100分,考试大纲可在报名网站查询。笔试成绩按照行政职业能力测验、申论、专业科目考试成绩分别占40%、30%、30%的比例合成。
报考法院系统、检察机关职位的,还须参加法律基础知识考试,分值100分,考试大纲可在报名网站查询。笔试成绩按照行政职业能力测验、申论、专业科目考试成绩分别占40%、30%、30%的比例合成。
报考其他职位的,笔试成绩按照行政职业能力测验、申论各占50%的比例合成。
2. 时间。公共科目笔试时间为2024年3月16日,专业科目笔试时间为2024年3月17日。具体安排为:
3月16日上午 9:00—11:00 行政职业能力测验
下午 14:00—16:30 申论
3月17日上午 9:00—11:00 公安类专业科目
上午 9:00—10:00 法律基础知识
报考者应当按照准考证上确定的时间和地点,同时携带准考证和本人有效居民身份证(与报名时一致)参加考试。
2024年重庆录用公务员考试专题>>>https://cq.huatu.com/zt/ztgwy/skgg/
——重庆公务员考试备考——
重庆公务员行测备考:数量关系之最值问题应该这样备考
行测备考:数量关系之最值问题应该这样备考
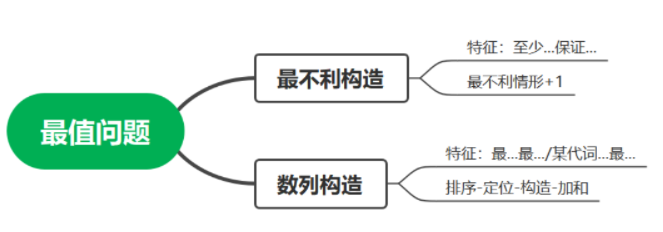
数量关系最值问题是公务员考试里面常考的题型之一,但是难度没有那么大,常见的最值问题包括两大题型,分别是最不利构造和数列构造。
题型一:看我如何搞定最不利构造
例1:某演唱会主办方为观众准备了白红橙黄绿蓝紫7种颜色的荧光棒各若干只,每名观众可在入口处任意选取2只,若每种颜色的荧光棒都足够多,那么至少( )名观众中,一定有两人选取的荧光棒颜色完全相同。
A.14
B.22
C.28
D.29
【答案】D
【解析】第一步,本题考查最不利构造。

例2:某会展中心布置会场,从花卉市场购买郁金香、月季花、牡丹花三种花卉各20盆,每盆均用纸箱打包好装车运送至会展中心,再由工人搬运至布展区。问至少要搬出多少盆花卉才能保证搬出的鲜花中一定有郁金香?
A. 20盆
B. 21盆
C. 40盆
D. 41盆
【答案】D
【解析】第一步,本题考查最值问题,属于最不利构造。 第二步,根据“至少……保证……”可知本题为最不利构造,答案为“所有最不利情况+1”。要求搬出的鲜花中一定有郁金香,最不利的情况是把所有月季花、牡丹花都搬出来,即搬出20+20=40(盆)。在此基础上再搬1盆,就能够保证搬出的鲜花中一定有郁金香,即至少要搬出40+1=41(盆)。 因此,选择D选项。
题型二:数列构造掌握规律也不难噢!
例1:从某物流园区开出6辆货车,这6辆货车的平均装货量为62吨,已知每辆货车载重量各不相同且均为整数,最重的装载了71吨,最轻的装载了54吨。问这6辆货车中装货第三重的卡车至少装载了多少吨?
A. 59
B. 60
C. 61
D. 62
【答案】B
【解析】第一步,本题考查最值问题,属于数列构造。 第二步,总和一定,求某项最值,使用数列构造的方法。首先,根据题意将6辆货车的载重量从大到小排序则第一重的为71吨,最轻的为54吨,求第三重的卡车至少载重多少,则其余货车载重尽量多,设第三重的卡车至少载重x吨,那么构造排名第二至第五的载重依次为:70,x,x-1,x-2。可列方程:71+70+x+(x-1)+(x-2)+54=62×6,解得x=60。 因此,选择B选项。
例2:某高校计划招聘81名博士,拟分配到13个不同的院系,假定院系A分得的博士人数比其他院系都多,那么院系A分得的博士人数至少有多少名?
A. 6
B. 7
C. 8
D. 9
【答案】C
【解析】第一步,本题考查最值问题中的数列构造问题。 第二步,总共招聘81名博士,要想院系A分得的博士数最少,则应构造其余院系分得的博士数尽可能多。设院系A分得博士x名,那么其余12个院系最多均有x-1名,可列方程:x+(x-1)×12=81,解得x≈7.2,那么院系A分得的博士至少有8名。 因此,选择C选项。
原文标题:2023河南省考行测备考:数量关系之最值问题应该这样备考
文章来源:河南华图教育(MD5:ef187fac1abe43894ea108d3c8da12f9)











