数量关系
数量关系题目难?答不完?小编为大家介绍数量关系中常见的蒙题大法,会让你在数量关系这一模块事半功倍。
数字特性秒杀法

数字的奇偶特性是指奇数与偶数在做数学加减乘除四运算时,不同组合产生的不同奇偶数字结果之间的规律。主要包括两条基础规律和两条推论:
【基础】奇数±奇数=偶数;偶数±偶数=偶数;偶数±奇数=奇数;
偶数×偶数=偶数;偶数×奇数=偶数;奇数×奇数=奇数;
【推论】
1. 任意两个数的和如果是奇数,那么差也是奇数;如果和是偶数,那么差也是偶数。
2. 任意两个数的和或差是奇数,则两数奇偶相反;和或差是偶数,则两数奇偶相同。
数字的奇偶特性主要运用在基础应用题涉及解不定方程的时候,但在数量关系题目考查内容越来越多元杂糅的现在,数字奇偶特性对解题效率的帮助也在更多题型中发挥着作用。例如下面这道几何问题:
【例2】一个长方形长6cm,宽4cm,现分别平行于长和宽剪了若干刀,将长方形分割成若干个小长方形,这些小长方形的周长之和比原长方形周长多了56cm。那么最多剪了()刀。
A.3 B.4
C.5 D.6
【答案】D
该题考查几何问题。解题时,先设平行于长剪了x刀,平行于宽剪了y刀,由题意可知:2(6x+4y)=56,化简为3x+2y=14。根据奇偶特性可知3x是偶数,那么x是偶数,当x=2时,此时y=4,共剪2+4=6刀;当x=4时,此时y=1,共剪4+1=5刀。可知最多剪了6刀。因此,选择D选项。
常识猜题法
常识猜题法即通过日常生活经验来判断正确答案。例如下面这道题:
【例3】某市某年末汽车保有量为50万辆,预计此后每年报废上一年末汽车保有量的5%,并且每年新增汽车数量相等。如要求该市汽车保有量不超过200万辆,那么每年新增汽车数量不应超过多少万辆?
A.2.5 B.5
C.7.5 D.10
【答案】D
根据日常生活经验,要保证保有量不超过200万辆,那么只需保证新增量不应超过报废量的最大值200×5%=10(万辆)即可。因此,直接选择D选项。
资料分析
资料分析时间紧、计算量大、题目多怎么破解?能“蒙”一道是一道,节约时间分配给稍难或者计算量较大的题目。
图形秒杀法
材料若是图形类,一般是柱状图、折线图,我们可利用高度替代具体数值,利用格尺比较大小。例如下面这道题:
【例4】
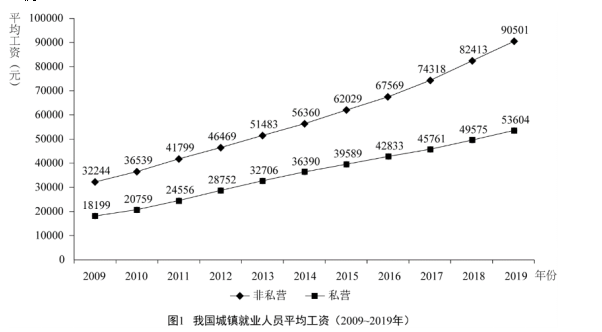
2009—2019年,城镇非私营单位和私营单位平均工资差额最大的年份是:
A.2009年B.2013年
C.2016年D.2019年
【答案】D
直接比较各年对应点之间的垂直距离,明显2019年最大。直接选出答案。
选项猜题法
很多资料分析题可以不通过复杂计算,只需要观察选项中与现有数据之间的联系,就能猜出正确答案。例如下面这道题:
【例5】2017年全国海洋生产总值77611亿元,比上年增长6.9%,海洋生产总值占国内生产总值的9.4%。
2017年,J省海洋生产总值为7217亿元,比上年增长9.2%,海洋生产总值占地区生产总值的8.4%,2017年,全省沿海沿江港口完成货物吞吐量20.4亿吨,同比增长8.3%;集装箱吞吐量1698.8万标箱,同比增长5.5%。
2017年J省海洋生产总值同比每增长1个百分点,当年其海洋生产总值约增加:
A.66亿元 B.72亿元
C.726亿元 D.776亿元
【答案】A
这道题的可利用选项猜出正确答案,思路如下:
首先,确定一下这道题的基本解题思路。这道题求1%的增量是多少,那基本思路是基期量(2016年J省的量)×1%即可得出。
其次,思路确定后,不着急求基期量,而是观察四个选项和材料中的数据,发现四个选项量级不同,我们从J省的现期量和增长率大小来推断基期量也是四位数,而四位数的1%不可能是百位数,直接排除了CD选项。
第三步,继续观察选项,发现B选项的72很大概率是由现期量(2017年J省的量)×1%得出的,可以排除,这样就能直接选出正确选项A。
这些“巧”招数你学会了吗?












