行测中的容斥问题一直以来都是学员的痛点,学员喜欢用公式去解这类题,然而对于复杂的容斥问题,只用公式是很难解题的。鉴于这种情况,笔者建议广大学员灵活运用容斥原理,结合画图法能够轻松解决容斥问题。
那么什么是容斥原理呢?很简单,多个集合(一般是两个或者三个)在计数的时候,不考虑重复的情况,先将各个集合的所有对象的数量“包容”进来,然后再把重复计数的数量“排斥”出去。下面,笔者将通过画图法对两种题型进行详细的讲解。
题型一:两集合容斥问题
两集合容斥问题抽象出来就是“符合A类,符合B类,A、B都符合”结合画图法表示如下:
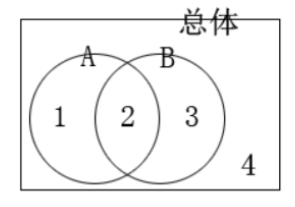
其中:A类的数量=图形1的面积+图形2的面积(简写成A=1+2)
B类的数量=图形2的面积+图形3的面积(简写成B=2+3)
图形1的面积=只符合A类的数量(符合A不符合B的数量)
图形2的面积=既符合A类又符合B类的数量(简称都符合)
图形3的面积=只符合B类的数量(符合B不符合A的数量)
图形4的面积=既不符合A类又不符合B类的数量(简称都不,有些题目中没有都不一项)
总体的数量=A+B-2+4
例1:某单位有60名运动员参加运动会开幕式,他们着装白色或黑色上衣,黑色或蓝色裤子。其中有12人穿白上衣蓝裤子,有34人穿黑裤子,29人穿黑上衣,那么穿黑上衣黑裤子的有多少人?
A. 12
B. 14
C. 15
D. 29
【答案】C
【解析】:第一步,本题考查容斥问题,属于二集合容斥类
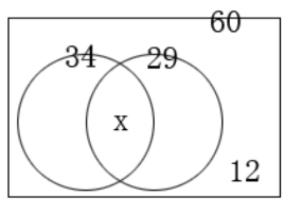
第二步,将穿黑裤子看成符合A类,将穿黑上衣看成符合B类,那么穿白上衣蓝裤子就是都不符合,而问题问的是都符合,设数量为x,运用画图法如下图所示即60=34+29-x+12,解得x=15。
因此,选择C选项。
例2:某公司100名员工对甲、乙两名经理进行满意度评议,对甲满意度的人数占全体参加评议的3/5,对乙满意的人数比甲的人数多6人,对甲乙都不满意的占对甲乙都满意人数的1/3多2人,则对甲乙都满意的人数是多少?
A. 36人
B. 26人
C. 48人
D. 42人
【答案】D
【解析】:第一步,本题考查容斥问题,属于二集合容斥类。
第二步,将对甲满意看成符合A类,将对乙满意看成符合B类,而问题问的是都符合设其数量为x,对甲乙都不满意的数量为x/3+2。
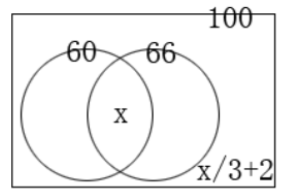
第三部,运用画图法如下图所示,即100=60+66-x+ x/3+2,解得x=42。
因此,选择D选项。
题型二:三集合容斥问题
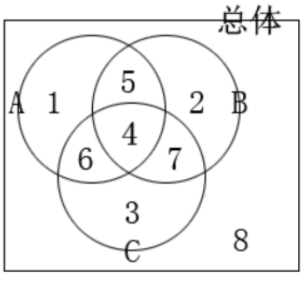
三集合容斥问题抽象出来就是“符合A类,符合B类,符合C类,都符合”结合画图法表示如下:
其中A类的数量=图形1 +图形4 +图形5积+图形6的总面积(简写成A=1+4+5+6)
B=2+4+5+7,C=3+4+6+7
图形1的面积=只符合A类的数量
图形2的面积=只符合B类的数量
图形3的面积=只符合C类的数量
图形4的面积=三类都符合的数量
图形8的面积=三类都不符合的数量(有些题目中没有都不一项)
考点1:4+5=既符合A又符合B的数量
4+6=既符合A又符合C的数量
4+7=既符合B又符合C的数量
考点2:5+6+7=符合两种类型的数量(即只符合两种类型的总数量)
总体的数量=A+B+C-(4+5)-(4+6)-(4+7)+4+8(考点1)
总体的数量=A+B+C-(5+6+7)-图形4面积的两倍+8(考点2)
例3:对39种食物中是否含有甲、乙、丙三种维生素进行调查,结果如下:含甲的有17种,含乙的有18种,含丙的有15种,含甲、乙的有7种,含甲、丙的有6种,含乙、丙的有9种,三种维生素都不含的有7种,则三种维生素都含的有多少种?
A. 4
B. 6
C. 7
D. 9
【答案】A
【解析】:第一步,本题考查容斥问题,属于三集合容斥类。
第二步,这道题属于三集合容斥问题考点1,把含有甲维生素看成符合A类,含有乙维生素看成符合B类,含有丙维生素看成符合C类,而问题问的是三类都符合的数量设为x。
第三步,运用画图法如下图所示,即39=17+18+15-7-6-9+x+7,解得x=4。
因此,选择A选项。
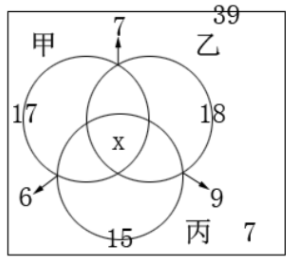
小结:此题属于考点1,画图标数的时候要注意符合A与B类,符合A与C类,符合B与C类区域,在图中分别用箭头把三个区域的不同数量标示出来,比如此题中的“含甲、乙的有7种,含甲、丙的有6种,含乙、丙的有9种”。
例4:某乡镇举行运动会,共有长跑、跳远和短跑三个项目。参加长跑的有49人,参加跳远的有36人,参加短跑的有28人,只参加其中两个项目的有13人,参加全部项目的有9人。那么参加该次运动会的总人数为多少?
A. 75
B. 82
C. 88
D. 95
【答案】B
【解析】:第一步,本题考查容斥问题,属于三集合容斥类。
第二步,这道题属于三集合容斥问题考点2,把长跑看成符合A类,跳远看成符合B类,短跑看成符合C类,而问题问的是总体的数量设为x。
第三步,运用画图法如下图所示即x=49+36+28-13-2×9,解得x=82。
因此,选择B选项。
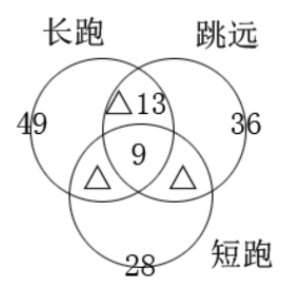
小结:此题属于考点2,画图标数的时候要注意只符合两种类型的区域,在图中总共有3个小区域,在这里可以标上符合△,表示△区域总面积为只符合两种类型的总数量,比如此题中的“只参加其中两个项目的有13人”。同时,这道题并没有给出都不符合的条件,故不需要画出最外边的方框。
例5:对某单位的100名员工进行调查,结果发现他们喜欢看球赛和电影、戏剧。其中58人喜欢看球赛,38人喜欢看戏剧,52人喜欢看电影,既喜欢看球赛又喜欢看戏剧的有18人,既喜欢看电影又喜欢看戏剧的有16人,三种都喜欢看的有12人,则只喜欢看电影的有多少人?
A. 22
B. 28
C. 30
D. 36
【答案】A
【解析】:第一步,本题考查容斥问题,属于三集合容斥类。
第二步,这道题属于三集合容斥问题的考点1,但是在此基础上加大了一点儿难度。把看球赛看成符合A,看戏剧看成符合B,看电影看成符合C,题目中没有给出都不喜欢这个条件,所以本题画图时不用画方框,并且缺少既符合B又符合C这个条件,所以常规解法受阻。
第三步,由于问题求的是只喜欢看电影的人数,即是求下图a中阴影部分面积,设其为x,运用画图法如下图b所示。图a中除开阴影部分,剩下部分面积即为求两集合容斥问题的数量,那么总面积=阴影部分面积+剩下部分面积。即100=x+(58+38-18),解得x=22。
因此,选择A选项。
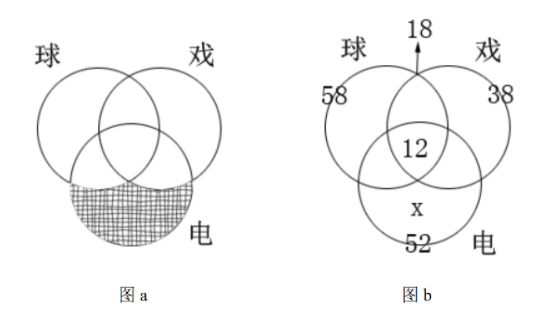
总结:这五道题充分利用了画图法的特性—直观性,使得解题过程极其简单,而且容易想到。所以笔者建议学员用画图法去解充斥问题,就再也不用纠结公式中字母的数学含义,能在做题的过程当中达到事半功倍的效果。
原文标题:2023国考行测数量关系备考干货之容斥问题
文章来源:华图教育(MD5:9b55b417ebaa20c81804f5e2534c15a8)










