众所周知,关于求基期量的公式有两个:一:基期量=现期量-增长量;二:基期量= false 。公式一作为一个加减计算相信大家操作起来游刃有余,公式二作为一个除法式子是值得我们花时间去研究和掌握一定速算技巧的。
接下来两个例子供大家思考,如果你拿到会怎么算?
【例1】 false ≈()
A.15.3万
B.16.7万
C.17.9万
D.19.4万
【例2】 false ≈()
A.124
B.126
C.129
D.132
拿到例1的第一直觉相信大家会马上想到直除 false ≈16.7万,此法做的确没问题也能选到答案,但再观例2会发现1-1.6%=0.984,124.3除以0.984相对较为难算,所以化除为乘法显得尤为重要。那到底什么叫化除为乘呢?下面为大家揭晓:
基期量= false = false = false ,当|r|≤5%, false ≤0.25%近似等于0,所以1- false ≈1,基期量=现期量×(1-r);
同理如果增长率为负,即基期量= false = false = false ,当|r|≤5%, false ≤0.25%近似等于0,所以1- false ≈1,基期量=现期量×(1+r);
所以大家不难发现,化除为乘的本质就是把运算符号全部进行一个改变,之后做题大家只用记住其本质:化除为乘,化加为减或化减为加。
这时我们再重温前两题,看能不能简单口算信手拈来。
例1: false =172167×(1-2.8%)=172167-172167×2.8%,而172167×2.8%大致估计约等于5000左右,172167-5000=167167,因此选择B选项。
同理例2: false =124.3×(1+1.6%)=124.3+124.3×1.6%≈124.3+2=126左右,因此选择B选项。

光说不练假把式,下面给大家两道考试真题让大家身临其境感受真实考场是如何考察我们的:
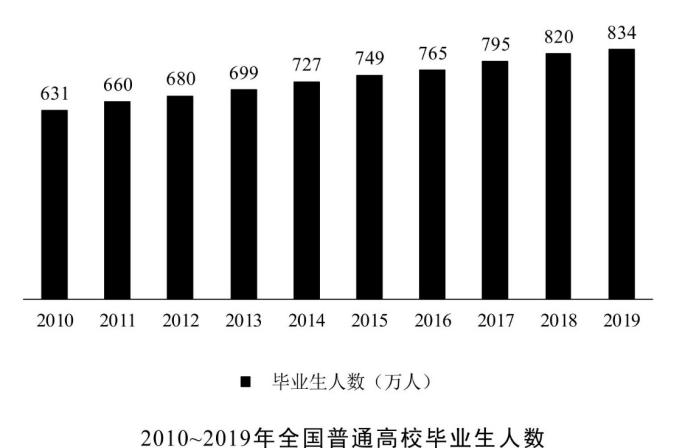
【例 1 】1979年全国普通高校毕业生人数为8.5万人,1980年为14.7万人,2001年为114万人,2002年为145万人,2010年较上一年同比增长3.4%,2018年首次突破了800万人,2019年预计达到834万人,毕业生就业创业面临严峻形势。
2009年全国普通高校毕业生人数约为( )。
A. 600万人
B. 610万人
C. 620万人
D. 630万人
解析:要求2009年 全国普通高校毕业生人数 ,定位柱形图2010年人数为631万 人,定位文字材料 2010年较上一年同比增长3.4% ,根据基期量= false 可得:2009年 全国普通高校毕业生人数 = false =631-631×3.4%≈631-20=611,因此选择B选项。
【例2】2016年6月份,我国社会消费品零售总额26857亿元,同比增长10.6%,环比增长0.92%。其中,限额以上单位消费品零售额13006亿元,同比增长8.1%。
2016年5月份,全国社会消费品零售总额约为:
24594亿元
B. 24283亿元
C. 26612亿元
D. 27104亿元
解析:要求 2016年5月份,全国社会消费品零售总额 ,定位文字材料 2016年6月份,我国社会消费品零售总额26857亿元,环比增长0.92%。 根据基期量= false 可得: 5月份全国社会消费品零售总额 = false =26857-26857×0.92%≈26857-268=26589,因此选择C选项。
本文通过简单朴素的除法式子让大家感受到了化除为乘的巧算魅力,你学会了吗?










