数量关系之赋值法
什么是赋值法呢?赋值法就是给某个量赋予一个具体的数值。比如说,我们小时候学过的,一项工程,甲工程队 好,说这里,老师需要同学们来思考两个问题。个问题,赋值法与方程来做需要10天。那甲工程队的效率就是十分之一,为什么是十分之一呢,因为我们给总成总量赋了1,所以他是十分之一,这在以前的学习中叫做化1法。我们也把它叫做,赋值法。
我们之前学过方程法,方程和赋值是有区别的,方程法是根据题意假设未知数。而我们现在要学习的赋值法,是给某个量赋予一个具体的值。所以方程和赋值法都是赋,方程赋的是未知数,而赋值法赋的是具体的数值。大家要了解他们之间的不同。


那么我们为什么可以使用赋值法,赋不同的值有区别吗?先说结论,并没有区别,我赋1,赋100,赋10000,没有任何区别。你赋多少都行,算出的结果都是一致的,赋不同的值对结果没有任何影响。为什么?因为我们赋的值,都可以约掉。这也是我们为什么可以使用赋值法的原因,对于我们较终结果是没有任何影响的。老师给大家举个例子,有一项工程,甲4天完成,乙5天完成,问合作需要多少天完成。我给工作总量赋20,那甲的效率就是20比4,乙的效率就是20比5,那合作就是20比甲的效率加乙的效率,我们发现赋的是20,但在列式的时候20都是可以约掉的,如果我们赋的是100,那100也可以约掉,如果赋的是200,也可以约掉。由于我们赋的值到较后都约掉了,所以我们赋多赋少并不影响较终的结果。所以我们在赋值的时候,什么数字好算就赋什么值。
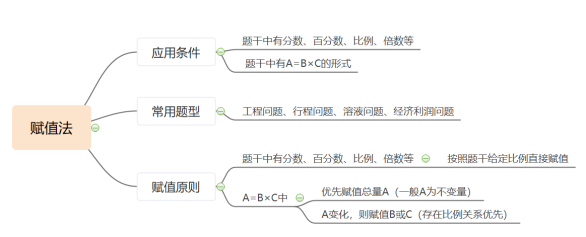
那么赋值法要怎么用呢?我们首先要明确它的使用范围,它在什么时候可以用。老师给大家做以归纳,一般呢,一个题目中,在题干会出现分数、百分数、比例、倍数等情况,这时候,我们就可以考虑使用赋值法帮助我们来做题。赋值时把可以把题目中的分数、百分数、比例、倍数化成较简分数。这是赋值法的个特点,同时题目中如果有A=B×C型的公式呈现,也可以使用赋值法。大家可能对于这样的形式不是特别理解,老师给大家列举一下这种形式的题型一般有工程问题,经济利润问题,行程问题,溶液问题,几何问题等。这几种问题有什么共性?我们说工程问题中,工作总量=效率×时间,经济利润问题中,总利润=单利润×销量,总收入=单价×销量。行程问题中,路程=速度×时间。溶液问题中,溶质=溶液×浓度。所有这些我们的适用题型,它都要有个通用的解题公式A=B×C型。都是要有三个量,且这三个量满足A=B×C的关系。
我们刚刚说了,题目中出现分数,百分数,比例,倍数等情况,可以赋值,为了好算,我们通常会按照题干中给出的这些比例来进行赋值,比如说甲乙的效率之比为3比2,我们赋值3和2,a和b兜里的钱数之比为4比5,那我们就赋值他们的钱为4和5。直接按照给定比例赋值就可以了。
接下来我们来看一个列题
例:将一批葡萄平均分装在36个箱子中,发现箱子没有装满,如果每箱多装1/8,则只需要使用箱子:
A.31个
B.32个
C.33个
D.34个
将一串葡萄平均分装在36个箱子中,发现箱子没有装满对吧?如果每多装1/8只需要使用多少个箱子?我们先看一下这道题,是不是他给了咱们分数啊?那么可以优先给他这分数赋值,他说多装1/8,那么我们赋值他第1次没有装满的时候装了8个。那么多装了1/8,就是装了多少呀?是不是9个呀?原来每个箱子平均装了8个,那么一共多少箱呢?36个箱子也就是36×8,现在是装9个再除以9。较后等于32个。
较后,我们来总结一下吧