关于恢复举行重庆市2022年度公开考试录用公务员笔试的公告
经研究,决定于2022年7月9日、10日恢复举行重庆市2022年度公开考试录用公务员笔试。考试科目及内容不变,具体考试时间及地点详见准考证。考生请于2022年7月5日上午9:00至7月10日上午10:00期间,登录报名网站打印准考证。如遇问题,请拨打网上报名技术咨询电话(023—86868837、023—86868838)。
为保障广大考生生命安全和身体健康,请考生按照要求填报本人考前14天内居住地详细地址(具体要求详见附件)。另外,市人事考试中心将于6月下旬在重庆市人力资源和社会保障局网站,发布《重庆市2022年度公开考试录用公务员笔试应试人员疫情防控须知》。请广大考生按照疫情防控相关要求,合理安排时间,提前做好相应准备,避免影响参加考试。
感谢广大考生的理解、支持和配合。
附件:关于完善重庆市2022年度公开考试录用公务员考试考生个人信息的通告
重庆市公务员局
2022年6月13日
附件
关于完善重庆市2022年度公开考试录用公务员考试考生个人信息的通告
为严格贯彻落实新冠肺炎疫情防控有关要求,全力保障考生健康安全,根据当前疫情防控工作需要,现就相关事项通告如下:
一、请考生于6月15日9:00至6月19日18:00期间,登录http://ggfw.rlsbj.cq.gov.cn/wsbm/wsbm_cqpta/index.html#/index,选择重庆市2022年度公开考试录用公务员考试项目,如实填报本人考前14天内居住地详细地址等相应信息,逾期未填报的,后期可能会影响正常参考。
二、凡隐瞒或谎报现居住地、旅居史、接触史、健康状况等疫情防控重点信息,不配合工作人员进行防疫检测、询问等造成不良后果的,取消考试资格;如有违法情况,将依法追究法律责任。
点击查看:2022全国公务员联考笔试重启时间汇总
>>>购买入口:2022重庆公务员招录考试考前冲刺试卷<<<
—— 重庆公务员备考 ——
2022重庆公务员考试数量关系备考:平面路径
平面路径
在平面几何中,我们常常会碰到与路径相关的问题,主要有三种表现形式:第一,对于给定的平面几何图形,如果已知起点和终点,按照指定的规则,求不同路径的数量;第二,对于给定的平面几何图形,要求走完每一段路,求最短路径;第三,计算平面图形中两点之间的最短距离。由于平面路径系列问题内容较多,计划分三次来给大家呈现,本次主要介绍第一类:
对于给定的平面几何图形,如果已知起点和终点,按照指定的规则,求不同路径的数量。一般通用的方式是逐点标数(本质为递推和数列)。具体方法:①确定起点和终点,在起点处标1;②确定运动方向(转化成上下左右)后转换角度,即每一点可能来的路径数;③由起点到终点(由近及远)逐级求和,每一个点的路径数等于可能到达它的点的路径数之和。理论比较抽象,我们通过几道例题一起来看一下:
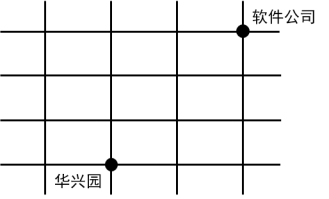
【例1】小张从华兴园到软件公司上班要经过多条街道(软件公司在华兴园的东北方)。假如他只能向东或者向北行走,则他上班不同走法共有:
A.12种
B.15种
C.20种
D.10种
【答案】D
【解析】
第一步,已知了起点和终点,并确定了向东和向北的运动方向,求不同走法的总数,采用逐点标数法。先在起点处标1,并在正东和正北方向标1,如下图:

第二步,除起点外,任何一点只能从它的左边和下边过来(因为要求路程最短),分析之后,接着可以标记余下点的路径数。如下图:
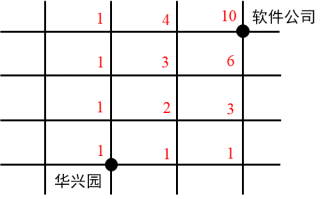
因此,选择D选项。
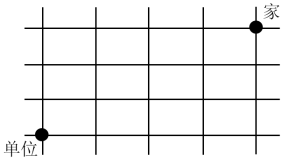
【例2】小赵从家出发去单位上班要经过多条街道(如图),假如他只能向西或向南行走。则他上班有多少种不同的走法?
A.6
B.24
C.32
D.35
【答案】D
【解析】
第一步,已知了起点和终点,并确定了向西和向南的运动方向,求不同走法的总数,采用逐点标数法。先在起点处标1,并在正西和正南方向标1,如下图:

第二步,除起点外,任何一点只能从它的上边和右边过来(因为要求路程最短),分析之后,接着可以标记余下点的路径数。如下图:
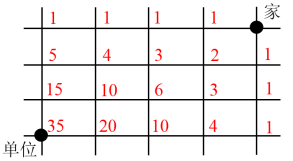
因此,选择D选项。

【例3】从A地到B地的道路如图所示,所有转弯均为直角,问如果要以最短距离从A地到达B地,有多少种不同的走法可以选择?

A.14
B.15
C.18
D.21
【答案】B
【解析】
第一步,已知了起点和终点,题干要求最短距离只能向右或向上行进,求不同走法的总数,采用逐点标数法。先在起点A处标1,并在正东和正北方向标1,如下图:

第二步,除起点外,任何一点只能从它的左边和下边过来(因为要求路程最短),分析之后,接着可以标记余下点的路径数。如下图:

因此,选择B选项。
【例4】A、B、C三地的地图如下图所示,其中A在C正北,B在C正东,连线处为道路。如要从A地到达B地,且途中只能向南、东和东南方向行进,有多少种不同的走法:

A.9
B.11
C.13
D.15
【答案】D
【解析】
第一步,已知了起点A和终点B,题干要求最短距离只能向南、向东或东南行进,求不同走法的总数,采用逐点标数法。先在起点A处标1,并在正南方向标1,如下图:

第二步,任何一点只能从它的上边、左边和左上方向过来(因为要求路程最短),分析明白之后,接着可以标记余下点的路径数。如下图:

因此,选择D选项。
对于平面几何中的路径类问题,即给定一个平面几何图形,已知起点和终点,按照指定的规则,求不同路径的数量的题目,虽然针对部分简单图形,排列组合可以使用,但并不是最常用的解法,我们最常用的解法是标数法(本质为递推和数列)。当然,需要各位同学把握好题目特征以及具体方法的操作步骤,只有熟练掌握才能灵活自如地运用。











