几何概率
近几年概率问题考查的越来越多,其中几何概率也随之成为一个小的热点模型。几何概率的本质非常简单,考试题目难度一般不大,如果掌握了几何概率的本质则很容易拿到这部分题目的分数。
先来看定义:如果每个事件发生的概率只与构成该事件区域的长度、面积或体积成比例,则称这样的概率模型为几何概率模型,简称为几何概型。


在圆形区域内考查几何概率比较多见,需要根据圆内各个半径计算面积的比值从而计算概率。2018年上半年多省市联考也考到了这样一道几何概率:
【例2】小波通过往圆圈里投掷米粒(米粒本身长度不计,视为一个点)的方式决定自己的周末活动。经过试验,他将米粒投进圆圈内的成功率达到100%,但投掷在圆内的位置随机。如果米粒到圆心的距离大于圆半径的一半,那么他周末去看电影;若米粒到圆心的距离小于半径的1/4,他会去打篮球;否则,他将在家看书。据此可知小波周末不在家看书的概率为:
A.13/16
B.2/5
C.3/5
D.1/16
【答案】A

【例3】将一长度为L的线段任意截成三段,设P1为所截的三线段能构成三角形的概率,P2为所截的三线段不能构成三角形的概率,则下列选项正确的是:
A.P1=P2 B.P1>P2
C.P1
【答案】C
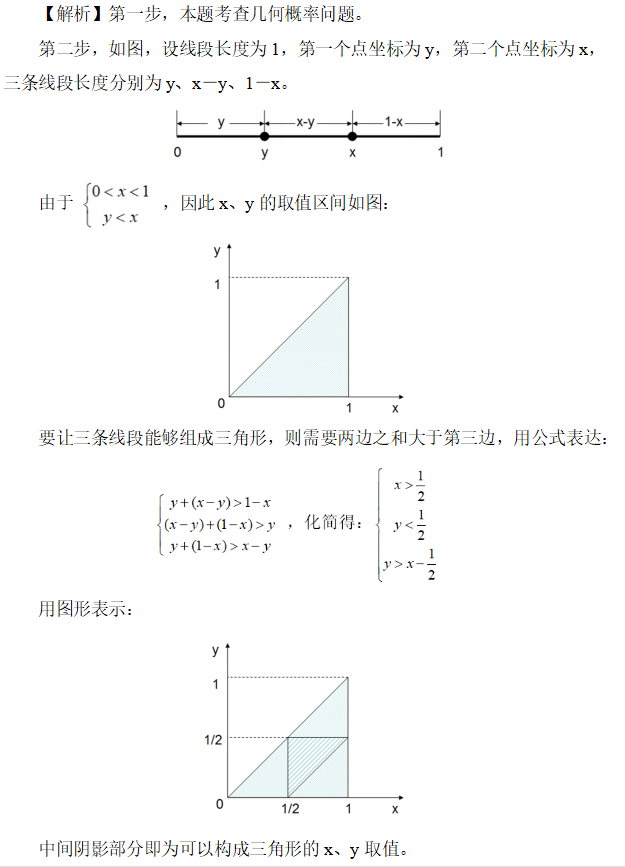
第三步,根据图形面积可知,能够构成三角形的概率P1为1/4,不能构成三角形的概率P2为3/4,则P1
因此,选择C选项。
本题难度十分大,但这道题在考场上也可以根据选项去选择:一根线段分成3截,两边之和与第三边的关系为:大于、等于或小于。三角形两边之和大于第三边、两边之差小于第三边,所以能构成三角形的概率小于不能构成的概率。
这种在直角坐标系里寻找几何概率的题目在公考中并不少见。无独有偶,2019年江苏考了一道与【例3】几乎一模一样的题目,只是选项更不好猜测。
【例4】将一根绳子任意分成三段,则此三段能构成一个三角形的概率是:
A.1/4 B.1/3
C.1/2 D.3/4
本题答案选择A,做法跟例3一模一样。本题难度很大,华图在线题库后台显示本题正确率只有18%。事实上可以根据选项相关,猜测答案为A、D中较小的那一个。
可以发现,几何概率如果给出了几何模型,就是简单的概率题目,必须拿分;如果需要在直角坐标系中自己构建模型,则可以根据选项猜测正确答案。在考场上不论什么方法,只要能选出正确答案,就是好方法。











