解决判断推理的这类难题,从这4个角度着手就够啦
近年来,随着考试难度的不断加大,要想在内卷越来越严重的道路上过关斩将,只学习基础的考点知识显然是远远不够的,那些偶尔出现的“疑难杂症”也应该应对自如,例如逻辑中的难点——集合推理。集合推理是一种边缘化考点,之所以把它称为边缘化考点,是因为这类考点并不是每年都会出现,但是一旦出现难度一般比较大,很多考生只能“望题兴叹”,这里就这类题的特点及做题方法谈谈自己的见解。
所谓集合推理,其实就是要求考生能够正确分析出集合概念之间的包含、被包含、相交、相离、推出等关系。搞清楚这些关系,才能对不同集合之间的推理关系灵活转化。对于集合推理的学习,我们需要从以下四个角度了解:四个基本,三个换位,两串推出和一个递推。接下来一一对这四个考点进行解析。
四个基本
四个基本,即集合所涉及的四个基本概念。在逻辑中,我们可以用A和B来表示两个集合,那么两个集合之间的关系就主要有四种:所有的A是B、所有的A不是B、有的A是B、有的A不是B。除此之外,还有两个个体的概念,即某个A是B,某个A不是B。如果用圈来表示集合概念之间的关系,那么这四个基本就可以用如下图示来表示:
(一)、所有的A是B,它有两种图示:
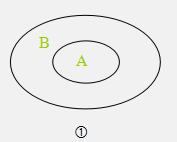
(二)、所有的A不是B,它只有一种图示:
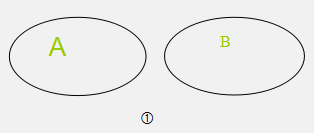
(三)、有的A是B,它有四种图示:
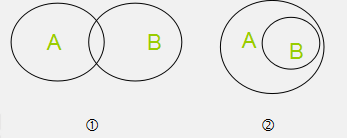
(四)、有的A不是B,它有三种图示:

三个换位
所谓换位,就是将A和B的位置进行调换,之所以要进行换位,是因为集合推理题目中,有的选项中给出的推出关系,题干中并没有涉及,那么要想推理,就必须换出选项中需要的集合关系,例如这道题目:“某科研机构的员工情况是:并非所有工程师都不是研究生,所有的工程师都是男性。根据以上陈述,可以得出以下哪项()
A.有的男性不是工程师
B.有的男研究生不是工程师
C.有的研究生是男性
D.有的研究生是女性”
这道题目中,题干只能得出:有的工程师→研究生,工程师→男性,而C项中说的是有的研究生→男性,“有的研究生”这个概念题干并没有涉及,因此必须通过换位的方式,换出一个“有的研究生”,因此就有了换位的必要,而换位也是集合推理的精髓所在。所谓三个换位,即:
(一)“所有A是B”→“有的B是A”;
(二)“所有的A不是B”等价于“所有的B不是A”;
(三)“有的A是B”等价于“有的B是A”。
这些换位之所以能成立,主要是基于上述每种关系的图示,例如,“所有A是B”的图示①,就可以表述为“有的B是A”,但图示②就不能这样表述,所以第一个换位只能是推出关系;“所有A不是B”的图示只有一种,这个图示也可以表述为“所有B不是A”,因此,这两个关系换位以后是等价的;“有的A是B”的四种图示也可以表述为“有的B是A”,所以第三种换位也是等价的。
两串推出
所谓两串推出,即所有、有的、某个之间的关系,例如:所有男生都喜欢玩游戏;小明喜欢玩游戏;有的男生喜欢玩游戏,那么所有男生喜欢玩游戏→小明喜欢玩游戏,小明喜欢玩游戏→有的男生喜欢玩游戏,因此我们可以得到第一组推出关系:所有是→某个是→有的是;与之对应的,所有不是→某个不是→有的不是。
一个递推
一个递推就比较简单了,就是我们所熟知的连锁推理,S→P,P→Q,那就可以写成S→Q,同样,有的S→P,P→Q,那么就可以得到:有的S→Q。但是这里需要注意的是,两个P所代表的概念必须完全相同。
综上所述,在做集合推理题目时,先将题干简化进行翻译,如果无法直接推出答案,那我们就要想到将它们进行换位,从而得到正确的答案,当然要做到这一点,就必须熟知四个基本、三个换位,从而攻克集合推理的题目。虽然这类考点出题频次不多,但是失之毫厘谬以千里,只有不放过任何一个难点,才能在公务员路上战无不胜。