在公务员数量关系解题过程中,最常使用的方法无疑是方程法,广泛应用于基础应用题、工程问题、行程问题、经济利润问题、溶液问题、几何问题等比例类题型和容斥问题、最值问题等计数类问题中。
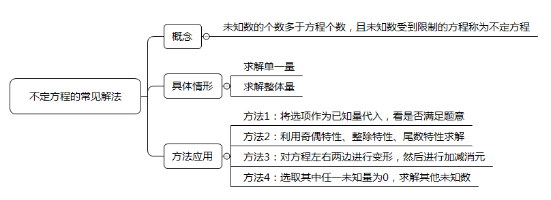
方程法的具体思路一般是根据题目的要求,选取一个或多个量设为未知数,然后找等量关系建立方程或方程组,接着求解未知数进而得到所求答案。由于题目的不同,在求解方程或方程组的过程中,一部分方程或方程组通过单纯的运算是没法直接求解出具体的未知数的,我们将这种未知数的个数多于方程个数,且未知数受到限制的方程称为不定方程。对于不定方程的常见解法,可以分为两种情况,具体如下表格:
| 类别 | 方法 | 应用 |
| 不定方程(组) (求单一量) | 代入排除法 | 将选项作为已知量代入,看是否满足题意,比如均为整数等 |
| 数字特性法 | 结合选项利用奇偶特性、整除特性、尾数特性求解 | |
| 不定方程组 (求整体量) | 消元法 | 对方程左右两边同时扩大一定倍数,然后进行加减 |
| 赋“0”法 | 选取其中任一未知量为0,求解其他未知数 |
接下来我们将通过几道例题,来进一步学习掌握不定方程的常见解法。
【例1】某儿童艺术培训中心有5名钢琴教师和6名拉丁舞教师,培训中心将所有的钢琴学员和拉丁舞学员共76人分别平均地分给各个老师带领,刚好能够分完,且每位老师所带的学生数量都是质数。后来由于学生人数减少,培训中心只保留了4名钢琴教师和3名拉丁舞教师,但每名教师所带的学生数量不变,那么目前培训中心还剩下学员多少人?( )
A.36 B.37
C.39 D.41
【答案】D
【解析】设每名钢琴教师、拉丁舞教师带领学员人数分别为x人、y人,所有学员共76人,建立等量关系:5x+6y=76。由于6y、76为偶数,那么5x一定也是偶数,进一步得出x为偶数,同时从题干可知x还是质数,在所有质数中只有2一个偶数,所以x=2,y=11,即每名钢琴教师带2名学员,每名拉丁舞教师带11名学员。由每名教师所带学生数量不变可得,剩余学员有4×2+3×11=41(人)。
【例2】某水果经销商到一山区水果基地采购猕猴桃和苹果。猕猴桃和苹果的采购价分别为10元/斤和4元/斤,销售价分别为25元/斤和12元/斤。已知该经销商在本次经销中获利40000元,每种水果采购都超过500斤且为整数。问该经销商的最佳投入资金是多少元?( )
A.20000 B.21260
C.21300 D.21280
【答案】B
【解析】设购买猕猴桃、苹果的重量分别为x斤、y斤,最佳投入资金为z元,由题干可
以建立等量关系:
,①化简为15x+8y=40000。由于8y和40000是8的倍数,则15x也应该是8的倍数,进一步可知x是8的倍数,同时要想投入的资金z最少,则x投入越少越好且必须大于500,则x=504,y=4055。则最佳投入资金为504×10+4055×4=21260(元)。
【例3】甲买了3支签字笔、7支圆珠笔和1支铅笔,共花了32元,乙买了4支同样的签字笔、10支圆珠笔和1支铅笔,共花了43元。如果同样的签字笔、圆珠笔、铅笔各买一支,共用多少钱?( )
A.21元 B.11元
C.10元 D.17元
【答案】C
【解析】 解法一(消元法):
设购买一支签字笔、一支圆珠笔、一支铅笔分别需要x,y,z元。由题干可以建立等量关系,,①×3-②×2=x+y+z=32×3-43×2=10元。
解法二(赋“0”法):
,令y=0,则x=11,z=-1,即x+y+z=10元。
通过上面3道例题的分析,可以清晰的看出,不定方程的求解是有一定的规律性的,求解单一量时代入排除法、数字特性法是常用的解题技巧,求解整体量时加减消元解题更加直接,但需要一定的数字观察能力,赋“0”法更好掌握但计算量大一些,在备考的过程中,大家可以结合使用,经过一定的练习之后,可以达到事半功倍的效果。
原文标题:2023上考行测数量关系技巧:不定方程常见解法
文章来源:华图教育(MD5:0bc9ad5707fbf0cc1dd2dfc121b104bb)










