数量关系是行测考试中常考的一类题型，但同时又是考生们最头疼的部分。很多考生对数量关系题目都畏之如虎，但是这并不意味着数量题目无法入手，比如说行程、工程以及不定方程中在任意范围内求解的题型都可以通过设特值的方法去求解。下面带大家一起来学习一下它。

　　定义

　　通过设题目中某些未知量为特殊值，从而简化运算的方法。

　　应用环境

　　1.题目中存在具有任意性的量。

　　2.题目中的概念间存在A×B=M的关系，且要求出其中一个，而另外两个未知。

　　例题展示

　　(一)行程题目

　　例1

　　甲从A地到B地需要30分钟，乙从B地到A地需要45分钟，甲乙两人同时从A、B两地相向而行，中间甲休息了20分钟，乙也休息了一段时间，最后两人在出发40分钟后相遇。问乙休息了多少分钟?

　　A.25 B.20 C.15 D.10

　　【答案】A。解析：设AB的距离是90，则甲每分钟走90÷30=3，乙每分钟走90÷45=2，由于甲走了40-20=20分钟，走的距离为3×20=60，则乙走的距离为90-60=30，用时为30÷2=15分钟，所以乙休息了40-15=25分钟，故选A。

　　(二)工程题目

　　例2

　　某新建农庄有一项绿化工程，交给甲、乙、丙、丁4人合作完成。已知4人的工作效率之比为3∶5∶4∶6，甲、乙合作完成所需时间比丙、丁合作多9天，则4人合作完成工程所需时间是∶( )。

　　A.17天 B.18天 C.19天 D.20天

　　【答案】D。解析：已知甲、乙、丙、丁工作效率之比为3∶5∶4∶6，设四人的效率分别为3、5、4、6，甲、乙合作完成所需时间为t天，则丙、丁合作完成的时间为t-9天，根据工作总量一定有(3+5)×t=(4+6)×(t-9)，解得t=45，工作总量为(3+5)×45=8×45，所求为8×45÷(3+5+4+6)=20天，故选D。

　　(三)不定方程题目

　　例3

　　现有甲、乙、丙三种货物，若购买甲1件、乙3件、丙7件共需200元;若购买甲2件、乙5件、丙11件共需350元。则购买甲、乙、丙各1件共需( )元。

　　A.50 B.100 C.150 D.200

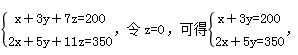
　　【答案】B。解析∶设购买甲、乙、丙各1件分别需花x、y、z元，则有上式×2-下式，可得y=50,代入上式可得x=50，因此所求x+y+z=50+50+0=100，即购买甲、乙、丙各1件需要100元，故选B。

　　以上就是关于用特值法去解决行程、工程以及不定方程的题目梳理，相信大家以后遇到同种类型题目的时候能想起用特值法去解决。

　　原文标题：2022河南省考行测数量关系：小小特值法，解决大问题

　　文章来源：河南华图教育(MD5：1e508bf7b62712da403090095cc2450e)