几何问题是每年常考的考点之一,很多几何问题可以结合因子特性,尾数特性,奇偶特性迅速解题。今天华图教育为大家整理了行测数量关系——巧解平面几何问题,希望能对各位考生有所帮助。
知识点回顾
公式:
三角形面积=1/2×底边长×高
长方形面积=长×宽
正方形面积=边长×边长
几何特性:
当三角形的底边相同,高之比等于面积之比
当三角形的高相同,底边之比等于面积之比
例题导入
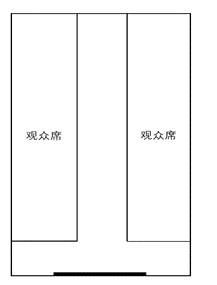
【例1】某单位要组织大家在体育馆观看建党100周年庆典,在布置长为20米、宽为18米的会场时,按照如图所示摆放板凳供员工入座,为了方便人员走动,在观影席前方和两侧观众席中间铺设了红地毯,铺设红毯的过道宽度一致,两侧观众席面积一致且和为288平方米,则过道宽度为多少米?
A.4米
B.3米
C.2米
D.1米
【答案】C
【解析】本题考查平面几何问题,找到题目中的等量关系,长方形的面积=长×宽,将两块观众席的面积拼成一块长方形,设过道宽为X。可得方程(20-X)×(18-X)=288。此方程为2次方程,考虑用技巧求解。观察式子发现20,18,288均为偶数,(20-X)×(18-X)要得到一个偶数,那么X必为偶数,排除B、D选项。剩A、C两个选项用代入排除,验证其中一个即可,代入A,(20-4)×(18-4)=16×14,得到尾数4的数,与最终结果尾数8对不上,因此排除A选项,选择C。
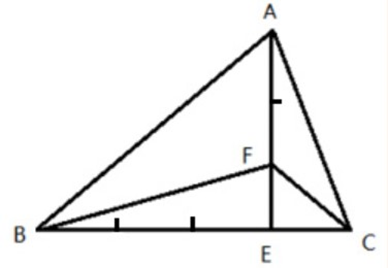
【例2】有一块三角形菜地,如下图,现计划将其分为四块区域种植不同蔬菜,如果BE=3EC,AF=2EF,三角形BEF和三角形AFC的面积之差为10平方米,则三角形ABC的面积为:
A.100平方米
B.120平方米
C.140平方米
D.150平方米
【答案】B
【解析】已知BE=3EC,AF=2EF,可得BE:EC=3:1,AF:FE=2:1。AE,BC分别为三角形的高以及底边长,那么底边长为4份,高为3份。根据三角形面积=,=6份,6里面含有因子3,因此问题所求三角形的面积应为3的倍数,排除A、C选项。又因为三角形BEF和三角形CEF有相同的高EF,所以底边之比等于面积之比,三角形BEF和三角形CEF面积之比为3:1,整个三角形BCF为4份。同理,三角形BFA和三角形CFA有相同的底边FA,则底边相同,高之比等于面积之比,高为BE和EC,所以面积之比为3:1,整个四边形BACF面积为4份。由于三角形BCF与四边形BACF面积构成了整个三角形ABC的面积,因此三角形ABC为4的倍数。排除D选项,选择B。

【小结】:今天这里提到的两种几何问题,主要围绕两个方向去解题。一、根据问题所得的式子推导出与选项相关的奇偶特性。二、根据题目中交代的比例关系,推出问题所求的量的倍数特性。
以下是思维导图,供大家参考:
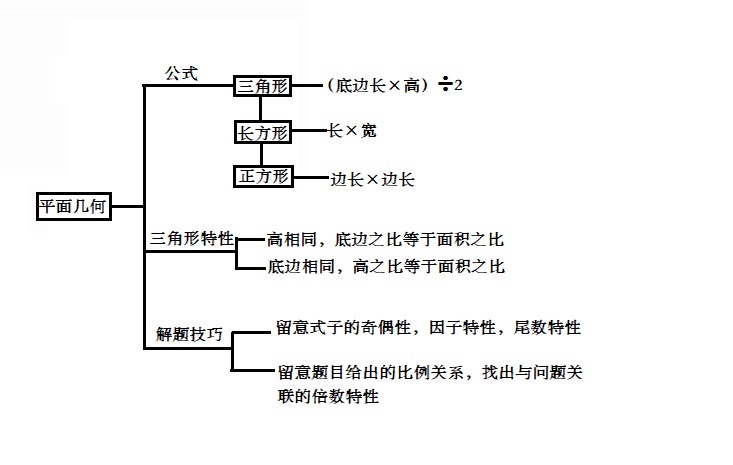
原文标题:2022年河南省考行测备考技巧干货:数量关系巧解平面几何问题
文章来源:河南华图教育(MD5:b8e202cf33e61c3d3a32e00a8c5c0ce0)










