2022重庆公务员考试公告已经发布

　　一、查询招考职位

　　各招录机关的招考人数、具体职位、考试类别、资格条件等详见《重庆市2022年度公务员招考职位情况一览表》(附件1，以下简称《招考职位情况一览表》)。招考职位有专业要求的，统一参考《重庆市考试录用公务员专业参考目录》(附件2)。有关报考政策和报名网络技术等事宜，请参阅《重庆市2022年度考试录用公务员报考指南》(以下简称《报考指南》)。报考者如对招考职位中的专业、学历、学位、资格条件和其他报考条件有疑问的，可直接电话咨询招录机关。>>>职位表下载

　　二、提交报考申请

　　本次考试采取网上报名方式，按照以下程序进行。报考者登录重庆市人力资源和社会保障局网站(http:// rlsbj.cq.gov.cn/)首页“我要办”中的“人事考试网上报名”栏目，点击“2022年重庆市公务员招录考试网上报名入口”进入报名系统。报考者可在2022年2月21日上午9:00至2月26日上午9:00期间登录报名网站提交报考申请，报考者只能选择一个部门(单位)中的一个职位报名，报名与考试时使用的本人有效居民身份证必须一致。>>>点击报名

　　三、照片审核及审核结果查询

　　重庆市人事考试中心审核报考者上传的电子照片(jpg格式，20KB以下)是否符合报考要求，照片审核通过即视为报名通过;审核未通过的，可在2022年2月27日上午9:00前进行修改，等待重新审核。>>>照片调整

　　四、网上缴费

　　报考者须在2022年2月28日上午9:00前在报名网站进行网上缴费(笔试考务费每人每科50元)。建档立卡贫困家庭和城市低保家庭的报考者，根据报考指南中“重庆市2022年度考试录用公务员笔试考试费免缴办理须知”办理。>>>缴费入口

　　五、打印报名信息表

　　缴费完成的人员应立即下载打印报名信息表并妥善保存，以备现场资格审查时使用。>>>报名信息表

　　六、开考比例和指标调整

　　《招考职位情况一览表》对笔试开考比例作了明确规定，招考指标与报名人数比例须达到规定的笔试开考比例方可开考，达不到的则相应递减或取消招考指标。招考职位中“艰苦边远地区基层职位”未达到笔试开考比例的，可将笔试开考比例降低至1︰3。公安人民警察法医、队医职位以及监狱戒毒人民警察狱医、所医职位达不到规定比例的，可以开考且不递减指标，若报名人数少于招考指标时递减指标至报名人数。因报名人数达不到笔试开考比例而被取消招考的职位，由重庆市人事考试中心向该职位已缴费的报考者退费或征得本人同意后将其调整到符合报考条件的其他职位。

　　七、打印准考证

　　报名审核通过且缴费成功的报考者，请于2022年3月21日上午9:00至3月27日上午10:00期间，登录报名网站打印准考证。如遇问题，请拨打网上报名技术咨询电话。>>>准考证打印入口

　　八、笔试内容、时间及地点

　　笔试包括公共科目和专业科目，在考试内容上体现分类分级原则。公共科目包括行政职业能力测验和申论两科。其中，行政职业能力测验为客观性试题，申论为主观性试题，满分均为100分，具体详见《重庆市2022年度公开考试录用公务员公共科目考试大纲》。申论试卷分为“申论1”、“申论2”和“申论3”，行政执法类职位申论考试类型为“申论3”，乡镇机关职位申论考试类型为“申论2”，其他职位申论考试类型为“申论1”。具体安排为：

　　3月26日上午  9:00—11:00  行政职业能力测验 | 下午  14:00—16:30  申论

　　3月27日上午  9:00—11:00  公安类专业科目 | 上午  9:00—10:00  法律基础知识

　　报考者应当按照准考证上确定的时间和地点，同时携带准考证和本人有效居民身份证(与报名时一致)参加考试。>>>笔试课程

　　八、成绩查询

　　报考者可于2022年4月26日上午9:00后登录报名网站查询公共科目、专业科目笔试成绩，4月29日上午9:00后查询笔试最低合格分数线、进入现场资格审查人员名单等相关信息。>>>成绩查询入口

　　九、现场资格审查

　　现场资格审查在2022年5月6日至14日期间进行。进入现场资格审查的人员，须持有关证件资料，按照规定时间到指定地点参加现场资格审查。>>>资格审查

　　十、 体能测评

　　体能测评在2022年5月10日至14日期间进行，由招录机关会同同级公务员主管部门组织实施。>>>查看公告

　　十一、专业能力测试

　　专业能力测试在2022年5月10日至12日期间进行，由招录机关具体实施。专业能力测试分值100分，占面试总成绩的30%。>>>查看公告

　　十二、面试

　　面试时间为2022年5月15日至16日，由市公务员主管部门统一组织，各区县和市级部门具体实施。>>>面试课程

　　推荐：2022年重庆公务员考试公告解读峰会

　　推荐：2022年重庆公务员考试职位检索系统

　　推荐：2022年重庆公务员考试教材经典6本套

　　推荐：重庆公务员考试历年分数线匹配查询

　　近些年的公务员行测考试中，最值问题中的数列构造一直是数量关系这一模块考查的“常客”，在近几年的国考和省考都考到过，这个题型如果没有掌握相应解题技巧和思路的话，对于大家来说难度是比较大的。但是数列构造题型特征相对比较明显，解题套路非常固定，如果能熟练掌握相应的解题技巧和思路，考场拿分相对比较容易。下面就让我们一起来学习下数列构造这种题型的解题方法。

　　数列构造通常考查的是一种极端构造的解题思维，利用极值解题，就需要熟练掌握构造的思路和技巧。这类题目解题套路也是非常的固定，掌握技巧和思路其实很简单。首先我们需要大家知道这种题型的题型特征：问题中出现“最多……最多/少……”、“最少……最多/少……”、“排名第几……最多/少……”时。

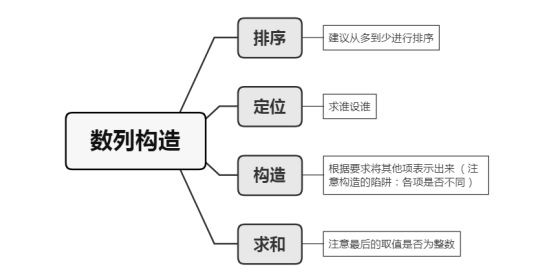
　　解题方法：排序——定位——构造——求和。接下来我们通过3道题来给大家详细说明这种题的解题思路和技巧。

　　【例1】现有21本故事书要分给5个人阅读，如果每个人得到的数量均不相同，那么得到故事书数量最多的人至少可以得到( )本。

　　A.5 B.7

　　C.9 D.11

　　【答案】B

　　【解析】第一步，识别题型，问题中出现“最多……最少……”特征，考查数列构造;

　　第二步，按照“排序——定位——构造——求和”四步解题，

　　排序：每个人得到故事书的数量均不相同，按照分得的故事书数量多少从多到少排序，就有1、2、3、4、5名;

　　定位：求谁设谁，根据问题“得到故事书数量最多的人至少可以得到多少本?”则让求的是得到故事书数量最多的人即求第一名有多少本，则设第一名为x本;

　　构造：根据要求将其他项表示出来，让求“得到故事书数量最多的人至少可以得到多少本?”即让第1名x最少，则让2、3、4、5名最多，第2名比第1名要少，则第2名最多比第1名少一本，为(x-1),第3名最多为(x-2),第4名最多为(x-3),第5名最多为(x-4);列表如下：

名次	1	2	3	4	5
数量	x	x-1	x-2	x-3	x-4

　　求和：根据总的书本数为21，可得x+(x-1)+(x-2)+(x-3)+(x-4)=21，解得x=6.2，即x至少为6.2，x为整数，所以得到故事书数量最多的人至少可以得到7本。

　　因此，选择B选项。

　　【例2】在一次竞标中，评标小组对参加竞标的公司进行评分，满分120分，按得分排名，前5名的平均分为115分，且得分是互不相同的整数，则第三名得分至少是( ) 。

　　A. 112分 B. 113分

　　C. 115分 D. 116分

　　【解析】第一步，识别题型，问题中出现“第几名……最少……”特征，考查数列构造;

　　第二步，按照“排序——定位——构造——求和”四步解题，

　　排序：每个人得分是互不相同的整数，按照得分的多少从多到少进行排序，就有1、2、3、4、5名;

　　定位：求谁设谁，根据问题“第三名得分至少是多少?”则让求的是第三名的得分，则设第三名得分为x;

　　构造：根据要求将其他项表示出来，让求“第三名得分至少是多少?”即让第3名x最少，则让1、2、4、5名都最多，第1名得分最多为满分120分，则第2名最多比第1名少一分119分,第4名最多比第三名少一分，为(x-1),第5名最多为(x-2);列表如下：

名次	1	2	3	4	5
得分	120	119	x	x-1	x-2

　　求和：根据前5名的平均分为115分，可得总得分为115×5，可得120+119+x+(x-1)+(x-2)=115×5，解得x=113，所以第三名得分至少为113分。

　　因此，选择B选项。

　　【例3】某单位2011年招聘了65名毕业生，拟分配到该单位的7个不同部门。假设行政部门分得的毕业生人数比其他部门都多，问行政部门分得的毕业生人数至少为多少名( )

　　A.10 B.11

　　C.12 D.13

　　【解析】第一步，识别题型，问题中出现“最多……最少……”特征，考查数列构造;

　　第二步，按照“排序——定位——构造——求和”四步解题，

　　排序：总共65名毕业生分到7个不同的部门，按照每个部门分的人数从多到少进行排序，就有1、2、3、4、5、6、7名;

　　定位：求谁设谁，根据问题“行政部门分得的毕业生人数至少为多少名?”行政部门分得的毕业生人数比其他部门都多，则让求的是第一名的得分，则设第一名得分为x;

　　构造：根据要求将其他项表示出来，让求“行政部门分得的毕业生人数至少为多少名?”即让第1名x最少，则让2、3、4、5、6、7名都最多，第2名人数最多比第1名少1人为(x-1)，这里要特别注意第3名到第7名的人数，题目中只说了行政部门分得的毕业生人数比其他部门都多，并没有说每个部门的人数都不同，所以第3名人数最多可以和第2名一样，为(x-1),同理，第4名人数最多可以和第3名一样，为(x-1),第4名人数最多可以和第3名一样，为(x-1),第5名人数最多可以和第4名一样，为(x-1),第6名人数最多可以和第5名一样，为(x-1),第7名人数最多可以和第6名一样，为(x-1),列表如下：

名次	1	2	3	4	5	6	7
人数	x	x-1	x-1	x-1	x-1	x-1	x-1

　　求和：根据总人数65人，可得x+(x-1)+(x-1)+(x-1)+(x-1)+(x-1)+(x-1)=65，解得x≈10.1，即x至少为10.1，x为整数，所以行政部门分得的毕业生人数至少为11人。

　　因此，选择B选项。

　　总结：从以上三个题目我们可以看到，数列构造的题型特征非常明显，解题套路同样非常固定，大家按照“排序——定位——构造——求和”四步解题，熟练掌握解题思路，另外在构造这一步要特别注意各项是否相同这个陷阱，最后的取值也要注意是否必须为整数，避免出现错误，数列构造考场上短时间内得分还是比较容易的。